Al aterrizar en la isla, desperté y vi que mis hermanos Diego y María seguían dormidos.
―¡Que ya hemos llegado!— les espeté. Diego ni se inmutó. María abrió un ojo, y me fundió con la mirada. Aún estábamos somnolientos cuando, a la salida del aeropuerto, nos interceptaron dos policías.
―Acompáñenme, por favor.— nos dijeron.
Mis padres, más despiertos que nosotros, no parecían preocupados. Los policías nos explicaron que en la isla no había monedas de curso legal y tendríamos que adaptarnos. Solo podríamos usar criptomonedas.
―¿Eso del bitcoin?— pregunté.
Asintieron. Nos dieron un folleto explicativo, que pasamos a leer con atención. Ahí se describía el bitcoin como una moneda digital, un tipo de dinero completamente virtual. Cada bitcoin es un archivo informático que se almacena en una aplicación de “monedero digital” en un dispositivo, tipo un móvil u ordenador.
Entonces esto no será muy complicado —dije a mis hermanos— La gente puede enviar bitcoins a su monedero digital, de manera que es sencillo enviar bitcoins a otras personas o comercios. Cada una de las transacciones se registra en una lista pública llamada cadena de bloques (blockchain, en inglés).
Seguí leyendo, sorprendido, que gracias a esto se puede rastrear el historial de Bitcoins para evitar que la gente gaste monedas que no posee, haga copias o deshaga transacciones.
—El blockchain— me explicó mi hermano— es una estructura de datos. Una cadena de bloques, donde cada bloque contiene un conjunto de transacciones. Una especie de libro de contabilidad distribuido que contiene todas las transacciones de forma cronológica; una red formada por muchísimos ordenadores comparten este libro.
—Y tantos ordenadores, ¿cómo se ponen de acuerdo?— preguntó mi hermana.
―Buena pregunta. A ver qué dice el folleto— contesté yo, ya algo impaciente
Según leímos, cuando alguien quiere hacer una transacción, digamos comprar algo, envía la petición a la red de ordenadores. Allá, unos ordenadores especiales llamados mineros, se encargan de ir recogiendo las peticiones (y hacer ciertas comprobaciones, como que tenga suficiente dinero para hacer la compra), y las incorporan a la cadena de bloques.
—Pero si hay tantos ordenadores, ¿quién se encarga de actualizar la cadena esa de bloques?— pregunté.
Pues se plantea un puzle, que es en realidad hacer un cálculo muy sencillo con ciertos valores, de modo que el resultado sea un valor que parece elegido al azar. Una versión simplificada sería por ejemplo pedirles calcular, para un primo p y dado un valor x, el cubo de x, y quedarse con el resto de calcular la división entera del cubo de x por p. Esto es, si x = 20 y p =541, el resultado sería 426, o si x = 21, con el mismo p, nos saldría 64.
—¿O sea que solo cambias un número y el resultado es completamente diferente?— preguntó María sorprendida.
—Del todo— observó Diego— Diferente e impredecible si no haces los cálculos, por eso se llama prueba de trabajo. Venga, os pongo a prueba, a ver quién es el que primero que encuentra un valor x que elevado al cubo y dividiéndolo por 541, proporcione un resto que acabe en cero.
Mi hermana y yo desenfundamos el móvil. A los pocos minutos, ella anunció el resultado con una gran sonrisa.
—¡El 36!
Mi hermano y yo comprobamos que estaba en lo cierto. 36 elevado al cubo es 46656, y al dividirlo por 541, el resto es 130.
—Y sólo os he pedido que acabe en un cero un 0— continuó mi hermano. Imaginaos si el objetivo es que con el mismo procedimiento acabe en dos ceros. ¿Lo queréis intentar?
Nuestros dedos se deslizaban por la pantalla con gran velocidad. En menos de un minuto, yo lo había conseguido
—¡El 481!— grité a los cuatro vientos. Mi estrategia de comenzar por el 540 e ir disminuyendo no había ido del todo mal.
De nuevo, comprobarlo fue unos pocos segundos, calcularlo, llevo bastante más trabajo. Ahora veía por qué se llamaba prueba de trabajo, pero aún nos faltaba entender cómo la cadena de bloques guardaba el dinero disponible de cada uno. En el folleto había una figura.
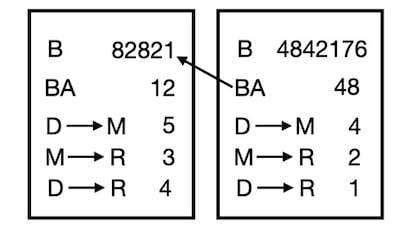
Cada rectángulo, decidimos, representaba un bloque. En cada uno, parecían reflejarse tres transacciones; por ejemplo, en el primer bloque interpretamos que D le ha dado a M 5 monedas M y D pagaban a R 3 y 4 monedas respectivamente. La etiqueta B podría ser una especie de nombre del bloque y el número junto a la etiqueta BA parecía hacer referencia al bloque anterior.
—¡Eyyyy!! ¿Os habéis dado cuenta de que son nuestras iniciales?— dijo mi hermana— Diego, Roger, María.
—Pues sí, quizá mucha casualidad— dije.
Como en los ejemplos del folleto el 541 jugaba el papel del divisor p, probamos a dividir 82821 entre 541, y, encantados, vimos que salía 48 . Ya sabíamos la relación cómo se construía la etiqueta BA del segundo bloque, pero ¿y B de dónde salía?
—¿Os habéis fijado que comienza por 48 y a continuación le siguen concatenados los 3 valores de las transacciones?—observó mi hermana.
—Mmmmmmm… pues ahora que lo dices, coincide totalmente— le contesté. Pero, ¿cómo se calculan los otros valores? Continuamos leyendo.
Ahí estaba la prueba de trabajo. Jugando con los números del folleto encontramos el puzle: había que calcular un número cuyos primeros dígitos fuesen 48421 tal que al elevarlo al cubo y calcular la división entera con 541, los dos últimos dígitos del resto fuesen 00. Y salía justo ¡4842176!
―Pues ya estaría —sentenció Diego—. El minero que consigue ese valor, lo anuncia; los demás mineros (como está haciendo María) comprueban que es correcto y, si están de acuerdo, se añade el bloque a la cadena.
Fuimos a los policías y les explicamos que ya lo habíamos entendido. La mujer policía sonrió misteriosa, nos dio un papel y preguntó ¿cuánto dinero tenéis cada uno?
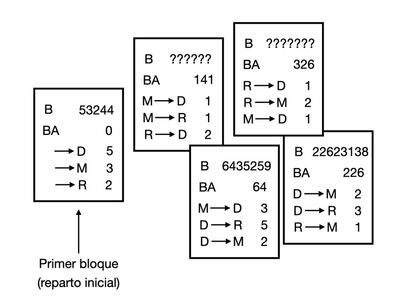
Conseguimos pasar la prueba, y con ella una pequeña recompensa que gastamos en una pizza, que costó, nada más y nada menos que 10.000 bitcoins. Corría el año 2010. ¡Y pensar que en euros esa pizza ha llegado a valer más de 500 millones de euros!
¿Conseguirías pasar tú también la prueba?
Los desafíos criptográficos se publicarán cada 15 días. Los lectores pueden dejar sus soluciones y debatir sobre el problema en los comentarios de esta página, por lo que se recomienda a quien quiera resolverlo por sí mismo no leerlos hasta haber descifrado el enigma. También pueden enviar sus respuestas al correo desafioscriptograficos@gmail.com. En cada nuevo desafío publicaremos la solución del anterior, acompañada de un comentario con algunas ideas originales o inspiradoras que hayamos recibido.
Vanesa Daza Fernández es profesora e investigadora del Departament de Tecnologies de la Informació i les Comunicacions de la Universitat Pompeu Fabra de Barcelona.
SOLUCIÓN AL DESAFÍO ANTERIOR
La herramienta criptográfica que aparece en este reto son los esquemas de compartición de secretos: cómo repartir un valor secreto s entre diferentes participantes, dando a cada participante Pi un fragmento fi, y de manera que sólo puedan recuperar el secreto a partir de sus fragmentos aquellos subconjuntos de participantes autorizados (que definen lo que se conoce como estructura de acceso).
En las dos primeras reparticiones del secreto (el código del candado), los subconjuntos autorizados eran todos aquellos con dos (o más) participantes. Es lo que se conoce como estructura de acceso de umbral (en este caso, el valor del umbral es 2). El criptógrafo israelí Adi Shamir (la S de RSA) propuso una manera segura de repartir secretos para una estructura de acceso de umbral t: se escoge un polinomio secreto, f(x), de grado t-1 que tenga como término independiente el secreto s, es decir
f(x) = s + a1·x + a2·x² + a3·x³ + … + at-1·x elevado a t-1
Y se asigna como fragmento de un participante Pi el punto del plano cartesiano (i,f(i)).
El polinomio secreto f(x) tiene t coeficientes desconocidos, s, a1,…,at-1. La intuición (y las matemáticas) nos dice que para encontrar esos t valores necesitamos saber al menos t datos de ese polinomio, por ejemplo su evaluación en t puntos diferentes. Si se tienen menos de t puntos / evaluaciones / fragmentos, cualquier polinomio de grado t-1 es posible, y por tanto el valor secreto s=f(0) queda completamente indeterminado.
En el caso de umbral 2, el polinomio tiene grado 1 y se corresponde a una recta, f(x) = s + a1·x. En el segundo reparto de fragmentos realizado por el Mago del Bosque, también correspondiente a una recta, tenemos que la recta que pasa por los puntos (1,15) y (2,17) es la recta de ecuación y = 2x + 13. Esa recta corta el eje OY en el punto (0,13), por tanto el secreto en ese caso era 13.
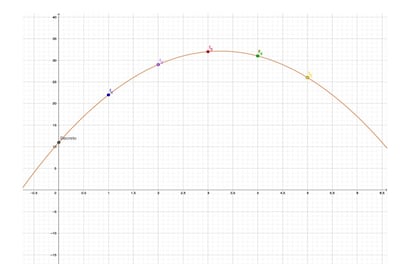
En el caso de umbral 3, el polinomio secreto tendrá grado 2, su gráfica será una parábola: f(x) = s + a1 x + a2 x².
Para recuperar ese polinomio (o parábola) secreto, hacen falta tres evaluaciones del polinomio, es decir tres fragmentos de tres reinos diferentes, por ejemplo tomaremos los Reinos 1, 2 y 3. Con esa información, plantearíamos un sistema de tres ecuaciones con tres incógnitas; las incógnitas son s, a1 y a2:
fragmento (1,22) -> 22 = f(1) = s + a1 · 1 + a2 · 1²= s + a1 + a2
fragmento (2,29) -> 29 = f(2) = s + a1 · 2 + a2 · 2²= s + 2 a1 + 4 a2
fragmento (3,32) -> 32 = f(3) = s + a1 · 3 + a2 · 3²= s + 3 a1 + 9 a2
La solución a ese sistema de ecuaciones es s=11, a1=13, a2=-2, es decir que el polinomio secreto era f(x) = 11 + 13·x – 2·x², y por tanto el secreto que abría el candado era s=11.
A partir de ese día, como serían necesarios t=5 fragmentos (es decir, todos los fragmentos de los cinco reinos) para recuperar el secreto, una posibilidad sería usar un polinomio secreto de grado 4. Pero hay otra posibilidad más sencilla y eficiente (y que funciona siempre que el umbral t sea igual al número total de participantes): dado un secreto s a repartir, el Mago del Bosque simplemente debía elegir cuatro fragmentos al azar, por ejemplo f1, f2, f3 y f4, y definir el último como f5 = s – f1 – f2 – f3 – f4. Así, la suma de los cinco fragmentos dará el secreto, pero con 4 o menos fragmentos no se obtendrá ninguna información sobre el secreto.
Cuando se usan esos esquemas para compartir secretos en la vida real, los secretos y los fragmentos no tienen tamaño libre, sino que por ejemplo se elige el secreto en el conjunto de enteros {0,1,2,3,…,q-1} para un número primo q, y se trabaja con operaciones modulares módulo q, es decir que q equivale a 0, q+3 equivale a 3, etc. Así se consigue que el tamaño de los fragmentos f(i) también esté controlado, puesto que pertenecen al mismo conjunto {0,1,2,3,…,q-1} que el secreto repartido.
Muchos de nuestros lectores (como Javier, Ramiro o Joaquín) han resuelto rápidamente este reto…asique os planteamos una pregunta adicional: otra opción que hubiese tenido el Mago del Bosque para hacer realidad el deseo de los Reinos 1, 3 y 4 de que el subconjunto {2,5} no pudiese recuperar el secreto, habría sido repartir el secreto para la estructura de acceso que contiene todos los subconjuntos de cardinal 2 excepto el {2,5}. ¿Os atrevéis a buscar la manera de repartir el secreto en ese caso?
PS: Tenemos pendiente de resolver también el desafío criptográfico musical que nos envió Salva Fuster en los comentarios a uno de estos retos. Ya hemos recibido alguna respuesta en nuestro correo desafioscriptograficos@gmail.com. Os animamos a resolverlo también. En el próximo desafío publicaremos la solución que nos ha remitido su autor.
Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.





