Todo aficionado a la Criptografía conoce la historia de cómo la inteligencia británica reclutó a ciudadanos de a pie en plena II Guerra Mundial a través de acertijos en el diario Daily Telegraph. Durante años, esos singulares criptoanalistas pelearon contra los cifrados alemanes en las cabañas de la Government Code and Cipher School, en Bletchley Park.
No pude evitar pensar en ello cuando Bernardo Marín, me pidió que coordinara para EL PAÍS el lanzamiento una serie de problemas criptográficos para desafiar el ingenio de los lectores. Con el auge de las nuevas tecnologías para la comunicación, la necesidad de expertos en Criptografía no es menos acuciante hoy que en los tiempos de Bletchley. Sin embargo, lejos de perseguir reclutar a nadie, nuestro objetivo era plantear un acertijo y, al mismo tiempo hacer divulgación: explicar de manera asequible algunos conceptos relacionados con la Criptografía moderna. Varios expertos entusiastas echaron mano de ingenio y diseñaron sus retos a base de mensajes cifrados en diferentes formatos, resúmenes imperfectos, criptomonedas, secretos en pedazos, estrategias para calcular probabilidades y hasta una prueba de conocimiento cero con barajas de póker.

Sin pretenderlo, hemos formado un pequeño escuadrón virtual de lectores que, a lo largo de casi cinco meses, se han atrevido con los diez desafíos. Algunos nos han hecho llegar sus ideas, han compartido sin pudor su frustración y, en ocasiones, nos han hecho ver nuestros errores e imprecisiones. Las respuestas recibidas en nuestra cuenta de correo delataban grandes diferencias de estilo, formación y conocimientos previos en Criptografía. Sorprendentemente, esa diversidad no fue tal en cuestión de género. Cuatro de los diez desafíos fueron planteados por mujeres, pero la gran mayoría de respuestas y comentarios recibidos han sido de hombres. No quiere decir necesariamente que ellas no hayan participado de los retos, pero sí que no han sido tan expansivas a la hora de compartir sus soluciones e interactuar con la comunidad de lectores.
Para aquellos que nos formamos en la era anterior al lenguaje inclusivo, el criptoanálisis se escribe en femenino. Tradicionalmente, cualquier esquema o protocolo criptográfico se planteaba involucrando a ciertos usuarios legítimos (Alice, Bob, Charlie…) enfrentados a la acción adversarial de una intrusa (típicamente llamada Eve o Tracy). Si bien la elección de esos nombres ficticios suele relacionarse con términos en inglés (Eve de eavesdropper, el que espía, Tracy de traffic analist, el que analiza el tráfico de comunicaciones), otras justificaciones son posibles. Yo elijo pensar que “Eva” representaba a una especie de heroína romántica, que blandía ante los peores conflictos herramientas matemáticas y computacionales (armas mucho más nobles y efectivas que aquellas reservadas para los combatientes masculinos). De ahí mi desazón al constatar que en nuestros Desafíos Criptográficos, Eva casi siempre ha sido él.
Concluimos este epílogo dando las gracias a todos los profesores que con su dedicación e ingenio han diseñado los retos; a nuestra ilustradora, Bel Martín, quien ha dotado de una estupenda personalidad gráfica a los desafíos; y, sobre todo, a los seguidores de esta sección por su fidelidad y esfuerzo; en especial, a aquellos que nos han escrito durante estos meses. Hemos aprendido y disfrutado tremendamente con vuestros mensajes; una vez más, a todos, gracias.
SOLUCIÓN AL DÉCIMO DESAFÍO
El reto de esta semana seguramente era uno de los más complicados. Pese a ello, hemos obtenido algunas respuestas interesantes e, incluso, una solución alternativa a la que habíamos identificado.
Esta es la solución que proponemos: una vez se ha completado la votación, las tres cartas bocabajo de la mitad izquierda se introducen en un sobre y lo mismo se hace con las otras tres cartas.

A continuación, los sobres se barajan de manera que ninguno de los votantes pueda saber cuál es cuál (esto puede conseguirse, por ejemplo, haciendo que un votante baraje mientras el otro tiene los ojos cerrados y viceversa).

Luego, se sacan las cartas de los sobres y se vuelven a colocar, en los espacios correspondientes, manteniendo el orden relativo de cada grupo de tres cartas. Así, las cartas pueden haberse quedado como estaban o haberse intercambiado, las tres de la izquierda con las tres de la derecha.

Seguidamente, se revelan las dos cartas de la fila superior.

Luego se revelan las dos cartas de la fila inferior que están en el lado del corazón de la fila superior. El orden de estas dos últimas cartas proporciona el resultado del protocolo.
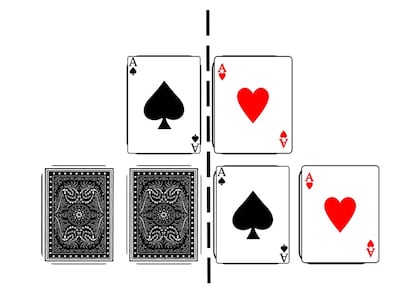
Por último, es importante darles la vuelta a todas las cartas y mezclarlas para que no se conozca el orden de las dos cartas que no se han revelado.
Este protocolo es un ejemplo recreativo (implementado con elementos físicos) de lo que en Criptografía se conoce con el nombre de protocolos de computación multiparte, que, en el mundo real, son algoritmos que se ejecutan en dispositivos electrónicos con capacidad de cómputo. En este tipo de protocolos, varias entidades tienen el objetivo de calcular una función que depende de un input o entrada secreta de cada una de las entidades. El objetivo del protocolo es que, sin intervención externa, el grupo de entidades sea capaz de calcular el output o salida de la función de forma que cada una de las entidades no obtenga información sobre las entradas del resto más allá de la que la propia salida proporciona. Nuestro ejemplo es un protocolo con dos partes en el que se calcula la salida de la función AND o conjunción lógica.
La clave del funcionamiento del protocolo está en observar que, para las cuatro configuraciones posibles de votos, las dos cartas de la fila inferior que están en el lado del corazón de la fila superior marcan el resultado deseado para el protocolo. En cuanto a la privacidad de los votos, está claro que revelar la fila superior no da información, ya que las dos cartas pueden haberse intercambiado o quedado como estaban. Si las dos cartas de la fila inferior se corresponden con “Cortar”, no hay problema, ya que está claro que ambos votantes han elegido “Cortar”. En cambio, si se corresponden con “Perdonar”, no hay manera de saber si estas dos cartas son las que se habían colocado al inicio o son el voto de la fila de abajo. Animamos al lector a que busque a alguien con quien probar a ejecutar el protocolo con materiales reales, ¡es muy divertido y puede incluso ayudar a tomar decisiones de forma colaborativa!
Se ha utilizado como referencia el artículo:
Kastner, J., Koch, A., Walzer, S., Miyahara, D., Hayashi, Y. I., Mizuki, T., & Sone, H. The minimum number of cards in practical card-based protocols. International Conference on the Theory and Application of Cryptology and Information Security (pp. 126-155). Springer, Cham. Diciembre, 2017.
Nuestro lector, Salva, nos ha propuesto una solución muy ingeniosa en la que se barajan las cartas de cada terna seleccionada, además de los sobres. Así nos lo explica:
Codificamos las cartas como R (as de corazones) y N (as de picas). La reina y el rey eligen el orden de sus cartas (RN: “Cortar” o NR: “Perdonar”) y las ponen boca abajo. Escogemos la primera carta de la reina, la primera del rey y la segunda de las añadidas, es decir, una carta R. Barajamos esas tres cartas y las metemos en un sobre, y también cogemos las otras tres cartas (la segunda de la reina, la segunda del rey y una carta N), las barajamos y las metemos en otro sobre. Posteriormente mezclamos los sobres para que no se pueda saber qué sobre contiene cada grupo de cartas.
En el caso de haber elegido la reina y el rey la opción “Cortar”, es decir, ambos el orden RN, al escoger las cartas de la manera indicada tendríamos en un sobre tres cartas rojas y en otro sobre tres cartas negras, de manera que al abrir un sobre y observar tres cartas del mismo tipo, sabríamos que la opción definitiva es “Cortar” (pero seguro que este no es el caso).
En cualquier otro caso en el que el resultado final es “Perdonar” (1. reina: RN, rey: NR; 2. reina: NR, rey: RN; 3. reina: NR, rey: NR), al escoger las cartas de la manera indicada tendríamos en un sobre dos cartas de un tipo y la otra del otro tipo, quedando en el otro sobre la opción complementaria, y como desconocemos el grupo de cartas escogido para cada sobre, no se puede saber la opción que han elegido la reina y el rey (ni siquiera entre ellos), pues lo único que se podría saber es que una/o (o ambos) ha(n) elegido “Perdonar”.
Puedes seguir a EL PAÍS TECNOLOGÍA en Facebook y Twitter o apuntarte aquí para recibir nuestra newsletter semanal.





