Podemos dividir nuestro triángulo obtusángulo de las últimas semanas en un mínimo de 7 triángulos acutángulos, tomando un punto interior de aquel como vértice común de 5 de estos, que forman un pentágono (¿puedes dibujarlo?). Como el pentágono es el menor polígono cuyos ángulos centrales pueden ser todos agudos, la división no es posible en menos de 7 acutángulos.
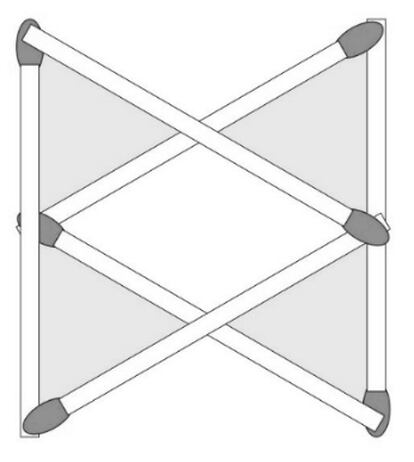
En cuanto a la formación de 4 triángulos equiláteros con 6 cerillas, en este tipo de problemas se suele pedir que se usen las cerillas en toda su longitud; pero como en este caso no se ha pedido (y precisamente venimos hablando de no imponernos más condiciones de las especificadas en el enunciado), a la clásica solución tetraédrica podemos añadir la de la figura, en la que los lados de los triángulos no son cerillas enteras sino medias cerillas. Y puesto que tampoco se pide que los triángulos sean 4 y solo 4, también es aceptable la solución propuesta por Bretos Bursó: “Si formamos dos triángulos equiláteros y los superponemos invertidos, formando una estrella de David, conseguimos una figura con 6 triángulos equiláteros”.
Y por lo que respecta al pentácoron, el análogo cuatridimensional del tetraedro, tiene 5 vértices, 10 aristas, 10 caras triangulares y 5 celdas tetraédricas.
El hipercubo, teseracto u octácoron, aunque es más complejo que el pentácoron, es más conocido y fácil de visualizar (es un decir), en buena medida por el Corpus Hypercubus de Dalí, y cualquiera que haya visto el cuadro sabe que tiene 8 celdas cúbicas (además de 16 vértices, 32 aristas y 24 caras cuadradas). En la figura vemos una típica representación bidimensional en perspectiva de una proyección tridimensional de un hipercubo, en la que es relativamente fácil contar los vértices, las aristas y las caras. Las 8 celdas cúbicas están representadas por el cubo grande, el cubo pequeño y las 6 pirámides truncadas cuyas bases mayores son las caras del primero y cuyas bases menores son las caras del segundo.

Jugando al póker con el arzobispo de Canterbury
El título de este artículo es el de un sorprendente libro recién publicado: El arte de la estadística, de David Spiegelhalter (Capitán Swing, 2023). Sorprendente desde el título mismo, puesto que la estadística es una rama de las matemáticas, una ciencia formal… ¿Puede considerarse también un arte?
El famoso economista John Maynard Keynes era muy dado a los experimentos mentales, y el más conocido de los suyos es, probablemente, el del concurso de belleza (una revista convoca un concurso de belleza en el que los lectores han de elegir, de entre las mujeres cuya fotografía aparece en sus páginas, a las seis más bellas; pero las premiadas no serán las mujeres más votadas, sino los lectores que más predicciones hayan acertado tras efectuar el recuento de votos).
No tan conocido, pero no menos interesante, es el de la partida de póker episcopal: imagina que estás jugando con el arzobispo de Canterbury y que en la primera ronda gana con una escalera real. ¿Pensarías que ha hecho trampa? La probabilidad de sacar una escalera real es bajísima (¿puedes calcularla?); pero, por otra parte, es inverosímil que monseñor arriesgue su prestigio sacándose cartas de la sotana.
Este tipo de reflexiones, en las que intervienen elementos subjetivos y conocimientos previos a la hora de estimar cuán probable es un suceso, llevaron al matemático y ministro presbiteriano Thomas Bayes, en el siglo XVIII, a replantear el cálculo de probabilidades de una forma tan novedosa como fecunda. El libro de Spiegelhalter es, entre otras cosas, una estimulante introducción a la estadística bayesiana. De la que habrá que seguir hablando en otras entregas, pues solo queda espacio/tiempo para el problema de rigor en relación con el asunto abordado:
Suponiendo que el 1 % de las mujeres tengan cáncer de mama y que las mamografías destinadas a detectarlo acierten en un 90 % de los casos (en el sentido de que el 90 % de las mujeres con cáncer y el 90 % de las mujeres sin cáncer sean diagnosticadas correctamente), ¿cuál es la probabilidad de que una mujer cuya mamografía dé positiva tenga realmente cáncer?
Puedes seguir a MATERIA en Facebook, Twitter e Instagram, o apuntarte aquí para recibir nuestra newsletter semanal.
Suscríbete para seguir leyendo
Lee sin límites





